[알고리즘] 크루스칼 알고리즘 + Python 구현
크루스칼 알고리즘은 Minimum Spanning Tree(최소비용 신장 트리)를 만드는 알고리즘입니다.
그 방법을 5개의 노드를 가지고 6개의 엣지를 가진 그래프를 가지고 단계별로 설명해보도록 하겠습니다.

일단 모든 엣지들의 정보를 비용의 정보를 토대로 오름차순으로 정렬해줍니다. (사실 내림차순 이어도 괜찮습니다.)
이렇게 정렬된 엣지들을 작은 순으로 하나씩 가져와서 사용할 것이기 때문입니다. 그리고 편하신 자료형으로
각 노드들의 부모 노드를 표시하게 만들고 일단은 자기 자신이 부모 노드가 되도록 초기화를 합니다.
이는 그래프에서 사이클이 발생했을 경우 그 엣지를 사용하지 않기 위함입니다.
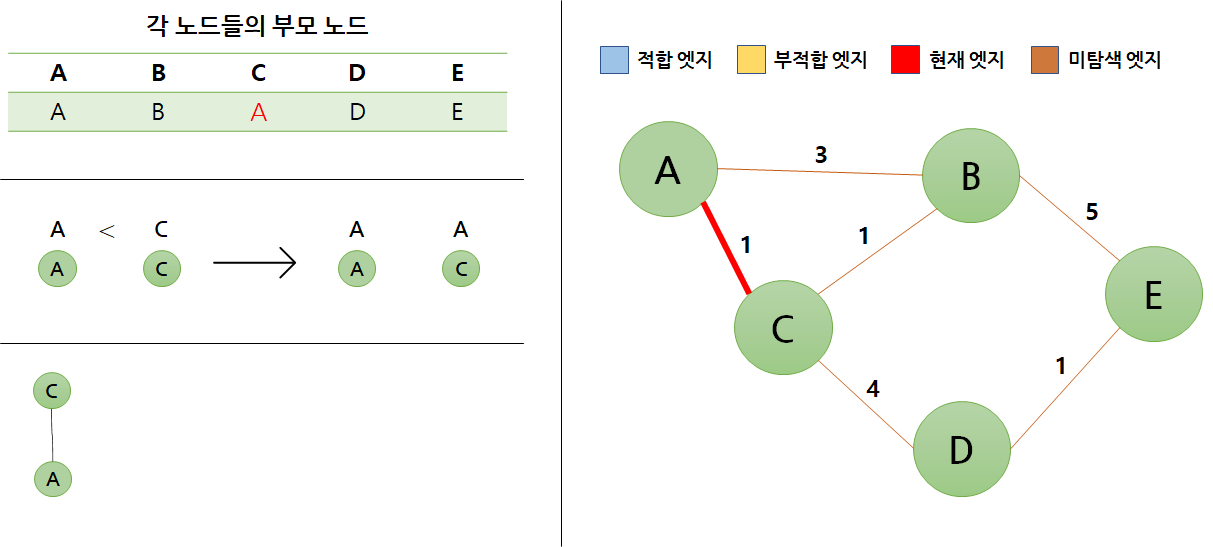
처음으로 가장 비용이 적은 엣지 중 하나인 A - C 에지를 가져오겠습니다.
- A - C에서 A와 C 노드의 부모 노드를 가져옵니다.
- 각 부모 노드들이 다르다면 통일 과정을 거쳐 작은 쪽의 부모 노드로 통일시킵니다.
- 이것이 뜻하는 바는 이 두 노드는 A라는 부모 노드를 가진 하나의 그룹이 되었다는 뜻입니다.
그럼 이제 다음 단계로 넘어가 봅시다.
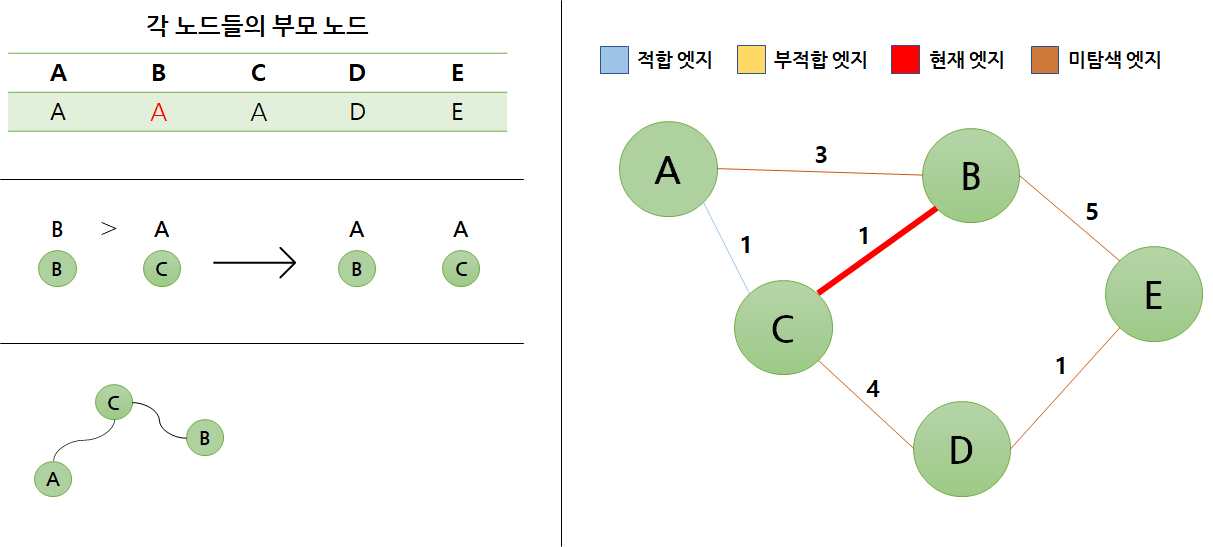
그다음으로 비용이 적은 엣지 중 하나인 A - C를 가져오겠습니다.
여기서도 위와 마찬가지로 B와 C의 부모 노드를 비교하여 A의 그룹에 B가 편입되었습니다.
C 의 부모 노드는 이전 단계에서 A로 변경된 상태였습니다.

비용이 1인 마지막 엣지 D - E를 가져오겠습니다.
여기서는 D와 E 노드 둘 다 A 그룹에 속하지 않습니다. 따라서 이 엣지는 새로운 D라는 그룹을 형성하게 됩니다.

이번에는 그다음으로 비용이 적은 A - B 엣지를 가져오도록 하겠습니다.
이번 경우는 조금 특이합니다. 지금까지는 한쪽만 그룹에 속해있거나 둘 다 속해있지 않거나 였다면
이번 엣지는 두 부모 노드 둘 다 A 그룹에 속해있습니다. 둘 다 같은 그룹에 속한 경우에는 엣지를 사용하지 않습니다.

만약 A - B 엣지를 사용하게 된다면 이미 C를 통하여 연결되어 있는 A와 B 노드를 다시 한번 연결하게 되어
사이클이 생기게 되고 이는 최소 비용이 아니게 됩니다. 그러므로 A - B 엣지는 사용하지 않습니다.

마지막이 될 C - D 노드를 가져옵니다.
만약 C 와 D의 노드는 서로 부모 노드가 A 와 D로 다릅니다. 이 경우에는 저희가 자주 보던 경우처럼 서로를 잇고
모든 그래프가 이어지게 되었습니다.

그런데 만약 여기서 노드가 더 있어서 E와 연결되야 하는 엣지가 있다면 어떻게 될까요? E의 부모노드는 아직 D입니다.
사실 여기서는 말씀드리지 않았지만 코드로 구현할때에는 부모 노드를 확인할때는 재귀 함수를 통하여
노드의 부모 노드가 자기 자신일 때까지 재귀 함수가 돌아가게 됩니다.
이제 크루스칼 알고리즘 원리는 많이 본 것 같습니다. 파이썬 구현 코드는 아래와 같습니다.
n = 5
graph = [
[1, 2, 3],
[1, 3, 1],
[3, 2, 1],
[2, 5, 5],
[3, 4, 4],
[4, 5, 1]
]
class Disjoint:
def __init__(self, n) -> None:
self.nodes = {x : x for x in range(1, n+1)}
def union(self, x, y):
if self.nodes[x] < self.nodes[y]:
self.nodes[y] = self.nodes[x]
else:
self.nodes[x] = self.nodes[y]
def find(self, x) -> int:
if self.nodes[x] == x:
return x
self.nodes[x] = self.find(self.nodes[x])
return self.nodes[x]
def kurskal(graph, n):
sorted_graph = sorted(graph, key=lambda x:x[2])
nodes = Disjoint(n)
length = 0
for link in sorted_graph:
if nodes.find(link[0]) != nodes.find(link[1]):
nodes.union(link[0], link[1])
length += link[2]
return length
print(kurskal(graph=graph, n=n))