
정렬 알고리즘을 공부하면서 앞의 정렬 알고리즘들은 가볍게 훑고 지나가도 되지만
이제부터는 집중해서 직접 구현해보고 이해하는 것이 좋습니다.
Merge Sort(합병 정렬)은 이 쪽 분야계의 천재 중의 천재로 불리는 존 폰 노이만이 개발했습니다.
합병 정렬은 특히 분할 정복 알고리즘으로 짜여진 알고리즘입니다.
분할 정복 알고리즘
문제를 풀기 쉽도록 분할 한 다음 나누어서 풀고 다시 합쳐서 해결하는 방법
이는 위의 그림만 보고는 헷갈릴 수도 있는데 아래의 링크를 보시면 쉽게 이해 될 것입니다.
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
[알고리즘] 합병 정렬(merge sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
너무 잘 설명해놓으셔서 이거를 뛰어넘는 설명은 못할 것 같습니다..
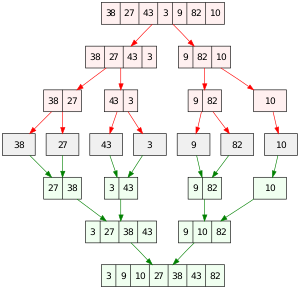
쉽게 말하자면 더 분해되지 않을때까지 쪼갠 다음 쪼갠 역순서대로 병합하면서 순서를 맞추는 형식입니다.
다만 위 그림과 달리 실제 구현 과정은 맨 위의 그림이 가장 적절해 보입니다.
또한 걸어둔 페이지 링크에도 정말 잘 설명된 그림이 있으니 꼭! 들어가서 확인해보시길 바랍니다.
input = [14,54,5,2,1,36,324,34,213,6,7,4]
def MergeSort(input):
# 자를 중간지점
cut_line = int(len(input)/2)
# 받아온 수열(데이터)가 길이가 1 초과일때
if len(input) > 1:
# 자르고 난 왼쪽 부분
left_side = MergeSort(input[:cut_line])
# 자르고 난 오른쪽 부분
right_side = MergeSort(input[cut_line:])
left_idx, right_idx = 0, 0
sorted_list = []
# left_side와 right_side에서 맨 앞 원소를 비교해가며 sorted_list에 삽입
while left_idx < len(left_side) and right_idx < len(right_side):
if left_side[left_idx] <= right_side[right_idx]:
sorted_list.append(left_side[left_idx])
left_idx += 1
else:
sorted_list.append(right_side[right_idx])
right_idx += 1
# 한 side에서 원소가 다 쓰였지만 반대 side에서 원소를 다 쓰지 못한 경우 삽입
while left_idx < len(left_side):
sorted_list.append(left_side[left_idx])
left_idx += 1
while right_idx < len(right_side):
sorted_list.append(right_side[right_idx])
right_idx +=1
# 데이터 길이가 1 혹은 0 일 경우 그대로 return
else:
return input
input = sorted_list
# 정렬된 list를 return
return sorted_list
print(MergeSort(input))아마 대부분의 경우가 재귀를 통해서 만드는 것이 제일 편할 것으로 느껴집니다.
left_side 와 right_side 병합시 각 맨 왼쪽(가장 작은) 원소를 비교해가며 작은 쪽은 넣고 idx를 증가 시킵니다.
저는 저 부분이 많이 헷갈려서 어떻게 짜야할지 초반에 당황했었네요.
'공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘 + Python 구현 (0) | 2021.07.17 |
|---|---|
| [알고리즘 공부] 5. Quick Sort (퀵 정렬) (0) | 2021.05.26 |
| [알고리즘 공부] 3. Insertion Sort (삽입 정렬) (0) | 2021.05.25 |
| [알고리즘 공부] 2. Selection Sort (선택 정렬) (0) | 2021.05.25 |
| [알고리즘 공부] 1. Bubble Sort (버블 정렬) (0) | 2021.05.25 |




댓글