알고리즘 문제를 풀 때 보면 시간 복잡도니, 공간 복잡도니, O(n)이니 무슨 소리인지 모르겠는 말이 많습니다.
Big O 그러니까 O(n) 같은 표시가 무엇인지 궁금해서 클릭하셨겠지만 시간복잡도랑 공간 복잡도부터 정리해보겠습니다.
시간 복잡도는 쉽게 말하면 들어오는 데이터 갯수 n에 대해 몇 번 연산을 하는가 라고 보시면 되겠습니다.
input_data = [x for x in random.sample(range(1000), 10)]예를 들어 위와 같은 길이 10 짜리 랜덤 수열이 생성 되고 (정렬 연산 없이) 가장 큰 수를 찾는다고 가정해봅시다.
그러기 위해서는 모든 수를 돌아봐야겠죠? 그러면 input_data[0]에서 input_data [9]까지 모두 돌게 될 것입니다.
주어진 데이터 n 만큼 도는 것이기 때문에 가장 큰 수를 찾는 알고리즘의 시간 복잡도는 O(n)이 되는 겁니다.
다만 시간 복잡도를 계산할때는 Best, Worst, Average 여러가지 경우가 있는데 이에 관해서는
https://memostack.tistory.com/57
시간 복잡도 (빅오, 빅오메가, 빅세타)
시간 복잡도란? 시간 복잡도는 특정 알고리즘이 얼마나 빠르게 수행이되는지 표현하기 위해 사용된다. 즉, 시간복잡도는 쉽게 말해서 알고리즘의 실행 시간을 말한다. 시간 복잡도의 종류 빅오
memostack.tistory.com
위의 블로그를 참조해주세요.
공간 복잡도는 더욱 단순합니다.
input_data = [x for x in random.sample(range(1000), 10)]
sort_data = []
for x in range(10):
sort_data.append(min(input_data))
input_data.remove(min(input_data))위의 코드는 조금 귀찮게(?) 오름차순으로 리스트를 정렬하는 코드입니다.
여기서는 변수로 원본인 input_data와 동일한 크기인 sort_data가 추가로 사용되었습니다.
이는 주어진 데이터 n 만큼의 메모리를 추가로 사용하였다고 하여서 총 공간 복잡도는 O(2n)이 되는 것이지요.
시간 복잡도와 공간 복잡도는 대체로 트레이드 오프의 관계를 가지고 있습니다.
시간 복잡도가 낮으면 공간 복잡도가 낮아진다거나 공간 복잡도가 낮아지면 시간 복잡도가 높아지는 형식이죠.
물론 모든 알고리즘이 그런 것은 아닙니다. 드물게 공간 복잡도, 시간 복잡도 둘 다 낮은 알고리즘이 있기도 합니다.
내가 짠 알고리즘은 공간, 시간 둘다 더럽게 잡아먹는 리소스 괴물
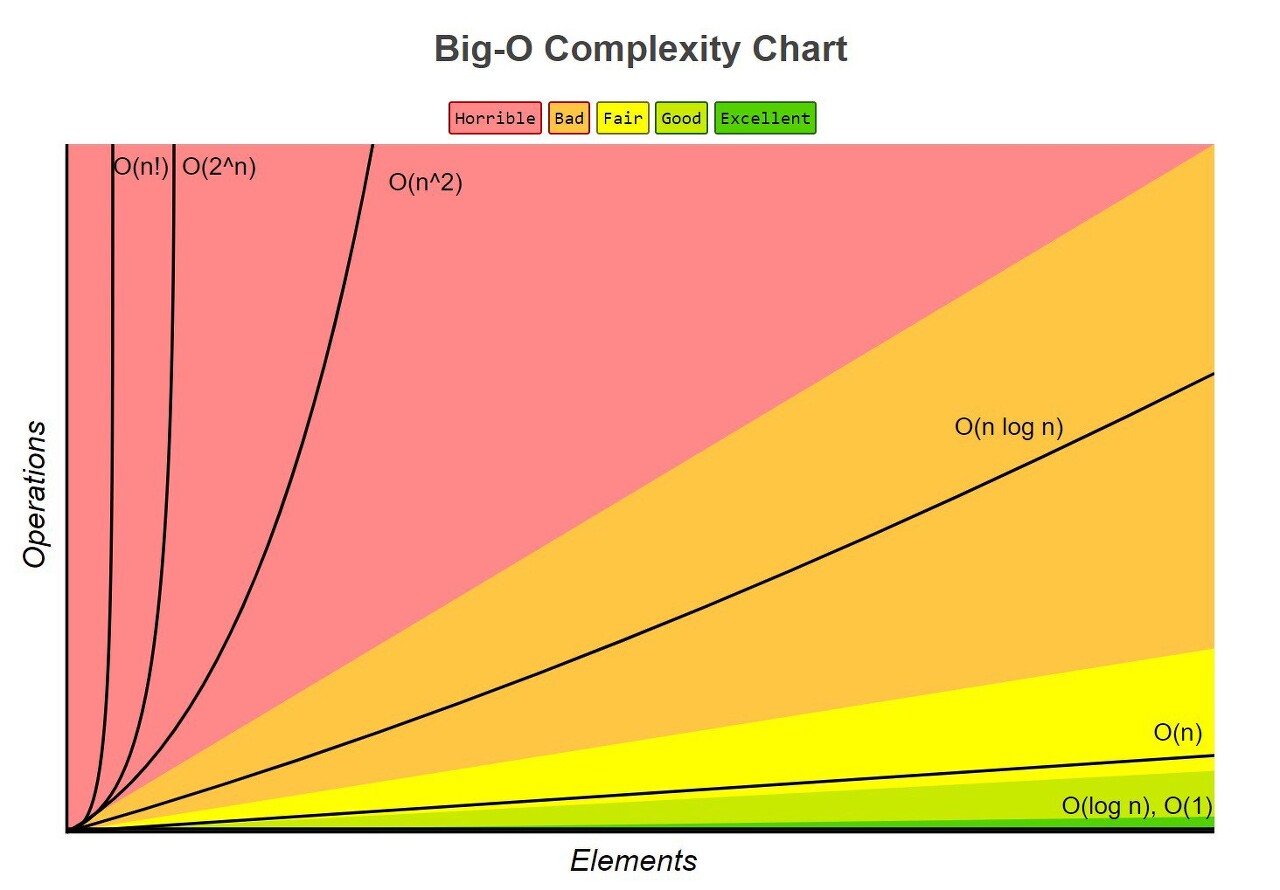
몇 가지 대표적인 시간 복잡도 표기가 있습니다 이를 빠른 순서대로 보자면
O(1) : 입력값이 아무리 커도 실행 시간은 일정한 최고의 알고리즘이라고 할 수 있지만, 상수의 값이 무한히도 크다면 이야기가 달라집니다. 해시 테이블의 조회 및 삽입이 이에 해당하는 알고리즘 중 하나입니다.
O(log n): 여기서 부터 입력값에 영향을 받는 실행 시간으로 로그는 큰 수에도 크게 영향을 받지 않으므로 뛰어난 시간 복잡도를 가지고 있다고 볼 수 있습니다. 이진 검색이 이에 해당하는 알고리즘입니다.
O(n) : 입력값 만큼 실행 시간이 영향을 받는 알고리즘으로 이러한 알고리즘을 선형 시간 알고리즘이라고 합니다. 여기서부터는 많은 알고리즘들이 해당하며 위 단락에서 말한 최댓값, 최솟값을 찾는 알고리즘도 O(n)입니다.
O(n log n) : 효율 좋은 정렬 알고리즘들이 포진한 시간입니다.
O(n^2) , O(2^n), O(n!) : 대체적으로 비효율적인 알고리즘들이 포진되어 있는 시간입니다.
각 시간들을 n에 따라 비교해보면 확연하게 차이가 납니다.
| 시간/n | 1 | 2 | 3 | 4 | 8 | 16 | 32 | 64 | 1000 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| log n | 0 | 1 | 1.58 | 2 | 3 | 4 | 5 | 6 | 9.97 |
| n | 1 | 2 | 3 | 4 | 8 | 16 | 32 | 64 | 1000 |
| n log n | 0 | 2 | 4.75 | 8 | 24 | 64 | 120 | 384 | 9966 |
| n^2 | 1 | 4 | 9 | 16 | 64 | 256 | 1024 | 4096 | 1000000 |
| n^3 | 1 | 8 | 27 | 64 | 512 | 4096 | 32768 | 262144 | 1000000000 |
| 2^n | 2 | 4 | 8 | 16 | 256 | 65536 | 4294967296 | 약 1844경 | 약 1.07 x 10301 |
| n! | 1 | 2 | 6 | 24 | 40320 | 20922789888000 | 약 2.63 x 1035 | 약 1.27 x 1089 | 약 4.02 x 102567 |
'공부 > 개념' 카테고리의 다른 글
| NoSQL 저장 유형별 간단 정리 (0) | 2021.06.06 |
|---|---|
| RDBMS, NoSQL, Elasticsearch 그리고 Hadoop (0) | 2021.06.04 |
| apache kafka 개념 정리 (0) | 2021.06.03 |
| [네트워크] TCP/UDP 간단 정리 (2) | 2021.05.30 |
| RESTful API 개념 정리 (0) | 2021.05.29 |



댓글